Double Averaging method
Contents
Quick summary
Date: 2007 (enhanced in 2020)
Developed by: Nikora et al., 2007 a and b (see references) (enhanced in the FIThydro project in 2020)
Type: Method
Introduction
The Double Averaging Method (DAM) is used for hydrodynamic variables and to provide simplified equations for the hydrodynamic modeling of flow similar to the Reynolds averaged Navier-Stokes equations (RANS), which are time-averaged. Over rough river beds flow structures are highly heterogenous. Therefore, they need to be resolved in detail instead of using simplified 2D assumptions, which is common within the RANS (Nikora et al. 2001). The concept of the DAM shall overcome this problem by taking into account the averaging over a certain area in addition to the averaging over time. This area should be chosen parallel to the river bed. The approach leads then to new equations of conservation of continuity and momentum.
The main advantages of the double-averaging approach include (Nikora et al 2007 a):
- a consistent link between spatially averaged roughness parameters, bed shear stress, and double-averaged flow variables
- explicit accounting for the viscous drag, form drag, form-induced stresses, and substance fluxes as a result of rigorous derivation rather than intuitive reasoning
- the possibility for scaling considerations and parameterizations based on double averaged variables
- the possibility for the consistent scale partitioning of the roughness parameters and flow properties, such as the bed shear stress.
However, the key limitation of this method is the need of a clear separation between turbulence and the mean flow on a wide enough scale.
A detailed explanatory derivation of the Double-Averaged Equations can be found for example within Giménez-Curto & Lera, 1996; Mignot et al., 2009; Nikora et al., 2001; Nikora et al., 2007 a and b.
Application
How can the DAM be applied?
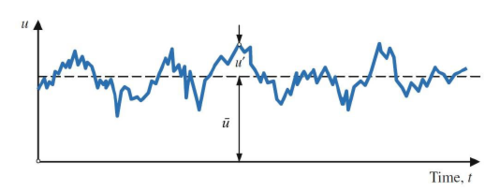
Turbulent flow is characterized chaotic - irregular in space and time. Hence, a statistical description needs to be used to define its properties. This can be done using the Reynolds-decomposition, which is a fundamental basis in characterizing turbulence: The measured instantaneous variable u is divided into the ensemble average ū (time-averaged) and the temporal fluctuation u', as illustrated in Figure 1.
Hence, the instantaneous variable is a combination of these parts. As a next step the time-averaged variable is also averaged in space, similar to the Reynolds-decomposition. This is most often done in planes zi parallel to the bed. The resulting instantaneous variable consists of the DA-value, the spatial fluctuation and the temporal fluctuation in the time-averaged flow variable:
θ(𝑥, 𝑦, 𝑧, 𝑡) = 〈θ̅ 〉(𝑧𝑖) +θ̃ (𝑥, 𝑦, 𝑧) + θ′(𝑥, 𝑦, 𝑧, 𝑡)
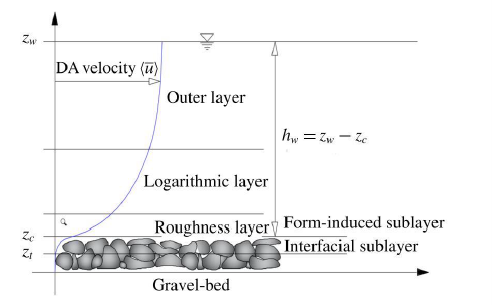
The overbar is the time-averaging operator. The angular brackets 〈 〉 are used as the space-averaging operator. The symbol ′ indicates temporal fluctuation, whereas the tilde (~) denotes spatial fluctuation. In order to investigate and classify the flow conditions in a rough river bed, Nikora et al. (2001) defined layer specifications (figure 2).
The flow is subdivided into three main layers according to the influence of occurring stresses: The top layer is called the outer layer, where bed roughness does not influence the velocity distribution. The next layer closer to the river bed is the logarithmic layer, where the distribution of the time-averaged velocity follows a logarithmic law. The logarithmic region does not reach until the roughness tops. The roughness layer is the first defined flow region to contain free flowing parts as well as the upper part of the roughness elements. In contrast to the other flow regions the roughness layer is influenced by the individual roughness elements of the river bed and therefore faces additional forces. It is subdivided into the form-induced sublayer just above the roughness crests and the interfacial sublayer which occupies the flow region between the troughs and the tops of the roughness elements. The form-induced sublayer was introduced because the flow is strongly affected by turbulences produced by the roughness crests which may appear as small eddies and causes an extensive spatial heterogeneity.
This is considered as the form-induced stresses in the Double Averaging momentum equation. In the case of a rough permeable bed, the layer below the roughness troughs is the last one and is named the subsurface layer.
Where can the DAM be applied?
The method allows to study the hydraulic conditions in natural environment hence in rough river beds. This includes for example . (Nikora et al 2007 b):
- identification of specific flow layers and flow types
- vertical distribution of the double-averaged velocity between the roughness tops and troughs
- vertical distribution of momentum fluxes and sinks for typical roughness types due to turbulence, mean flow heterogeneity, secondary currents, form drag, and viscous drag
- estimates of form induced - dispersive - stresses and evaluation of their structure using quadrant analysis
- closure development for mass-transfer uptake processes for stream periphyton
Relevant mitigation measures and test cases
Other information
Relevant literature
- Aberle, J., V. Nikora, M. Henning, B. Ettmer, and B. Hentschel. 2010. ‘Statistical Characterization of Bed Roughness Due to Bed Forms: A Field Study in the Elbe River at Aken, Germany: STATISTICAL CHARACTERIZATION’. Water Resources Research 46 (3). https://doi.org/10.1029/2008WR007406.
- Aberle, Jochen, Katinka Koll, and Andreas Dittrich. 2008. ‘Form Induced Stresses over Rough Gravel-Beds’. Acta Geophysica 56 (3): 584–600. https://doi.org/10.2478/s11600-008-0018-x.
- Coleman, Stephen E., Vladimir I. Nikora, and Jochen Aberle. 2011. ‘Interpretation of Alluvial Beds through Bed-Elevation Distribution Moments: ALLUVIAL-BED ANALYSIS AND BED-ELEVATION DISTRIBUTION MOMENTS’. Water Resources Research 47 (11). https://doi.org/10.1029/2011WR010672.
- Dey, Subhasish, and Ratul Das. 2012. ‘Gravel-Bed Hydrodynamics: Double-Averaging Approach’. Journal of Hydraulic Engineering 138 (8): 707–25. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000554.
- Ferraro, D., S. Servidio, and R. Gaudio. 2019. ‘Velocity Scales in Steady-Nonuniform Turbulent Flows with Low Relative Submergence’. Environmental Fluid Mechanics 19 (4): 1025–41. https://doi.org/10.1007/s10652-019-09663-3.
- Ferraro, Domenico, Sergio Servidio, Vincenzo Carbone, Subhasish Dey, and Roberto Gaudio. 2016. ‘Turbulence Laws in Natural Bed Flows’. Journal of Fluid Mechanics 798 (July): 540–71. https://doi.org/10.1017/jfm.2016.334.
- Giménez-Curto, Luis A., and Miguel A. Corniero Lera. 1996. ‘Oscillating Turbulent Flow over Very Rough Surfaces’. Journal of Geophysical Research: Oceans 101 (C9): 20745–58. https://doi.org/10.1029/96JC01824.
- Mignot, Emmanuel, E. Barthelemy, and D. Hurther. 2009. ‘Double-Averaging Analysis and Local Flow Characterization of near-Bed Turbulence in Gravel-Bed Channel Flows’. Journal of Fluid Mechanics 618 (January): 279–303. https://doi.org/10.1017/S0022112008004643.
- Nikora, Vladimir, Derek Goring, Ian McEwan, and George Griffiths. 2001. ‘Spatially Averaged Open-Channel Flow over Rough Bed’. Journal of Hydraulic Engineering 127 (2): 123–33. https://doi.org/10.1061/(ASCE)0733-9429(2001)127:2(123).
- Nikora, Vladimir, Ian McEwan, Stephen McLean, Stephen Coleman, Dubravka Pokrajac, and Roy Walters. 2007 (a). ‘Double-Averaging Concept for Rough-Bed Open-Channel and Overland Flows: Theoretical Background’. Journal of Hydraulic Engineering 133 (8): 873–83. https://doi.org/10.1061/(ASCE)0733-9429(2007)133:8(873).
- Nikora, Vladimir, Stephen McLean, Stephen Coleman, Dubravka Pokrajac, Ian McEwan, Lorna Campbell, Jochen Aberle, Dougal Clunie, and Katinka Koll. 2007 (b). ‘Double-Averaging Concept for Rough-Bed Open-Channel and Overland Flows: *Applications’. Journal of Hydraulic Engineering 133 (8): 884–95. https://doi.org/10.1061/(ASCE)0733-9429(2007)133:8(884).
- Papadopoulos, Konstantinos, Vladimir Nikora, Stuart Cameron, Mark Stewart, Hamish Biggs, and Christopher Gibbins. 2016. ‘Time-Averaged Hydrodynamic Equations for Mobile-Bed Conditions’. In Hydrodynamic and Mass Transport at Freshwater Aquatic Interfaces: 34th International School of Hydraulics, edited by Pawe\l Rowiński and Andrea Marion, 1–9. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-27750-9_1.