Acoustic Doppler velocimetry (ADV)
Contents
Quick summary
Developed by: Several companies (e.g. Nortek, SonTek)
Date: 1994
Type: Device
Introduction
Acoustic Doppler velocimetry (ADV) is a velocity measurement technique that allows for the measurement of 3D flow velocities by using the Doppler shift principle. ADV operates by emitting short acoustic pulses along a transmitter beam, the central transducer. As the sound bursts propagate through the water, a fraction of the acoustic energy is scattered back by ambient scatterers such as suspended sediments and microbubbles (Kraus et al. 1994, Lohrmann et al. 1995, McLelland & Nicholas 2000).
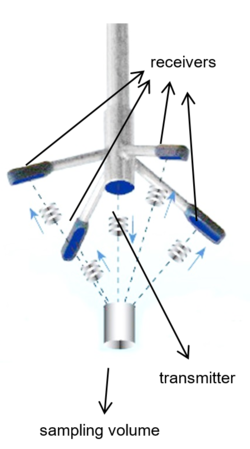
The ADV comprises a probe connected to the main housing, which contains the electronics, by either a rigid stem or a cable (Figure 1, 2 and 3). The main housing is connected to a computer by a cable. The sampling volume is located away from the probe (Figure 4), which reduces the interference of the probe with the flow and measurement point. The reduced probe size also minimizes the flow interference. The probe consists of a transmitter and three or four receivers (Figure 2 and 3), which are equally angled and symmetrically arranged around the transmitter (Khorsandi et al. 2012). The fourth receiver provides redundancy improving turbulence measurements. The transmitter emits ultrasound (short acoustic pulse) at a known frequency and the receivers get back the echo of ultrasound (sound-scattering particles) reflected in the water particles with a different frequency. The difference between the frequency emitted and reflected is proportional to water velocity.
The signal-to-noise ratio (SNR) is a measure of the scattering strength, representing the strength of the echo relative to the electronic noise level, and it is a central parameter in ADV operation (Kraus et al. 1994). The acoustic echoes originated at the sampling volume, defined by the intersection of the transmitter and receivers beams (Figure 4), are detected by the receivers’ transducers. The frequency of the echo is Doppler shifted according to the relative motion of the scatterers, assumed to be travelling with the velocity of the fluid flow. The Doppler shift observed at each receiver is proportional to the component of the flow velocity along the bisector of the receiver and transmitter beams. The radial or beam velocities are computed sequentially for each receiver and are then converted to a local Cartesian coordinate system (ux, uy, uz) by using a transformation matrix. This transformation matrix is determined empirically by the manufacturer by calibrating the system at one speed and will remain constant if the physical dimensions or geometry of the probe remain unchanged (Kraus et al. 1994, Lohrmann et al. 1995, McLelland & Nicholas 2000).
The ADV uses a dual pulse-pair scheme with different pulse repetition rates separated by a dwell time (McLelland & Nicholas 2000, García et al. 2005). The longer pair of pulses is used for higher precision velocity estimates while the shorter pulse is used for ambiguity resolution, assuming that the real velocity is beyond the limit resolvable by the longer time lag (García et al. 2005). The pulse repetition rates can be adjusted by choosing the instrument velocity range.
It is a widely used technique due to its capability to measure the three components of instantaneous velocities, its robustness and portability, the fact that it does not require calibration and its relatively low cost (Khorsandi et al., 2012, Quaresma et al., 2017). It is also suitable for laboratory and field applications.
ADVs capability of accurately measuring time-averaged velocities has been referred by Lemmin & Rolland (1997), Voulgaris & Trowbridge (1998), Quaresma et al. (2017). On the other hand, the quality of turbulence quantities computed from ADV data has been questioned, and the need for post-processing emphasized (Hurther & Lemmin 2001, Goring & Nikora 2002, Blanckaert & Lemmin 2006, Cea et al. 2007, Parsheh et al. 2010, Khorsandi et al. 2012, Montero et al. 2014, Quaresma et al. 2017). Moreover, it is a point-wise measurement technique, therefore, obtaining maps of time-averaged turbulent flow variables involves placing one single probe in several successive positions, which is time-consuming, or deploying multiple probes (which may be too expensive and impractical) (Quaresma et al. 2017).
It is known that the precision of ADV measurements in turbulent flows is affected by random spikes, including sampling errors linked with analogue/digital conversion, and the Doppler ambiguity process, characterized by the amplitude modulation of the backscattered signal related to the transit time of the acoustical targets through the sampling volume (this error is independent of the flow and depends on the pulse length, set by the velocity range), Doppler noise (which is intrinsic to the measurement principle and is associated with the random motion of targets in the sampling volume), and errors due to the mean velocity gradients in the sampling volume and associated to spatial averaging of the instantaneous flow field within the sampling volume and unresolved turbulent scales that are of the same order of magnitude or smaller than the sampling volume’s transverse size (Garbini et al. 1982, Voulgaris & Trowbridge 1998, McLelland & Nicholas 2000, Hurter & Lemmin 2001, Goring & Nikora 2002, Khorsandi et al. 2012). The spatial averaging of fluctuating motion contributes to reducing the variance of the signal; all the other sources of error contribute to increasing it (Hurter & Lemmin 2001).
In recent years several papers have been focusing on the theoretical and experimental identification and characterization of noise sources affecting the turbulence measurements performed with ADV (Garbini et al. 1982, Lohrmann et al. 1994, Voulgaris & Trowbridge 1998, McLelland & Nicholas 2000, Hurther & Lemmin 2001, García et al. 2005). Even when all the manufacturers’ precautions are taken into consideration, the signal will have a noise level that affects the values of turbulence parameters (García et al. 2005).
Several post-processing filters have been proposed to reduce the effect of noise resulting from random spikes, namely the phase-space thresholding despiking method of Goring & Nikora (2002), the velocity correlation filter of Cea et al. (2007), and the modified phase-space thresholding despiking method of Parsheh et al. (2010).
On the other hand, the Doppler noise is “white” noise with a Gaussian probability distribution and a flat power spectrum (McLelland & Nicholas 2000, Hurther & Lemmin 2001, García et al. 2005). White noise does not affect the mean velocity values because it has zero mean. Lohrmann et al. (1994), Voulgaris & Trowbridge (1998) and McLelland & Nicholas (2000) showed that the ADV can accurately predict mean velocity and Reynolds shear stresses.
Hurther & Lemmin (2001) proposed a correction method for subtracting the contribution of noise from the mean turbulent parameters. This method takes advantage of the bistatic four-receiver configuration of some ADV instruments, and consequent redundancy in the measurements of the velocity along the axis of the ADV. The variance of the noise and the noise spectrum can thus be determined. The geometrically weighted noise spectrum is then subtracted from the spectra of the longitudinal components. Turbulence intensities are obtained by integration of the latter.
Application
ADV has been extensively used in flow field characterization in fish migration and fishways studies. Odeh et al. (2002) used ADV to characterize flow turbulence to evaluate its effects on the behaviour of downstream migratory juvenile fish. Puertas et al. (2004) and Liu et al. (2006) conducted ADV measurements to characterize flow patterns and turbulence structures of flow in vertical slot fishways laboratory scale models. To assess the effects of water velocity and turbulence on the behaviour of Iberian barbel in an indoor full scale experimental pool-type fishway with orifices, Silva et al. (2011) used ADV measurements. Also in an indoor full scale experimental pool-type fishway with orifices, Santos et al. (2012) assessed the effect of two flow regimes, created by boulder placement in the flume bottom, in the upstream movements of Iberian barbel by performing ADV measurements to characterize the flow field. Branco et al. (2013) used ADV to characterize the water velocity and turbulence to evaluate the behaviour of two different morpho-ecological cyprinid species facing plunging and streaming flows in an indoor full scale experimental pool-type fishway with orifices and notches. To characterize a vertical slot fishway turning pool flow and validate a CFD model Marriner et al. (2014) performed ADV measurements on the Vianney-Legendre vertical slot fishway in Quebec, Canada. Bombač et al. (2015) performed extensive field measurements of the flow in a VSF, at the Arto – Blanca hydropower plant, and used these measurements to calibrate and verify a CFD model. To assess the effects of hydrodynamics on fish behaviour, and evaluate the upstream passage performance of a potamodromous cyprinid, over an experimental broad-crested weir, Amaral et al. (2016) characterized the flow pattern downstream of the weir with ADV. An et al. (2016) validated a three-dimensional CFD model of a VSF by carrying out velocity measurements in a physical model with ADV. Romão et al. (2017) used ADV measurements to characterize the flow hydrodynamics in an indoor full-scale pool-type fishway for two different vertical slot configurations. Quaresma et al. (2018) used these data to calibrate and validate a three-dimensional CFD model subsequently used to compare the hydrodynamics of two widely used vertical slot fishways (VSF) configurations and three multi slot fishway (MSF) configurations.
Relevant mitigation measures and test cases
Other information
WinADV, a free Windows-based viewing and post-processing utility for ADV files (Wahl, 2000) is widely used to post-process ADV data. The Multi-instrument turbulence toolbox (MITT) Open-source MATLAB algorithms for the analysis of high-frequency flow velocity time series datasets from MacVicar et al. (2014), is also available for the post-processing of ADV data.
Relevant literature
- Amaral SD, Branco P, Silva AT, Katopodis C, Viseu T, Ferreira MT, Pinheiro AN & Santos JM. 2016. Upstream passage of potamodromous cyprinids over small weirs: the influence of key-hydraulic parameters. Journal of Ecohydraulics 1:79-89. https://dx.doi.org/10.1080/24705357.2016.1237265
- An R, Li J, Liang R & Tuo Y. 2016. Three-dimensional simulation and experimental study for optimizing a vertical slot fishway. Journal of Hydro-environment Research 12:119-129. https://dx.doi.org/10.1016/j.jher.2016.05.005
- Blanckaert K & Lemmin U. 2006. Means of noise reduction in acoustic turbulence measurements. Journal of Hydraulic Research 44(1):3–17. https://dx.doi.org/10.1080/00221686.2006.9521657
- Bombač M, Novak G, Mlacnik J & Četina M. 2015. Extensive field measurements of flow in vertical slot fishway as data for validation of numerical simulations. Ecological Engineering 84:476-484. https://dx.doi.org/10.1016/j.ecoleng.2015.09.030
- Branco P, Santos JM, Katopodis C, Pinheiro A & Ferreira MT. 2013. Pool-Type Fishways: Two Different Morpho-Ecological Cyprinid Species Facing Plunging and Streaming Flows. PLoS ONE 8(5):e65089. https://dx.doi.org/10.1371/journal.pone.0065089
- Cea L, Puertas J & Pena L. 2007. Velocity measurements on highly turbulent free surface flow using ADV. Experiments in Fluids 42(3):333–348. https://dx.doi.org/10.1007/s00348-006-0237-3
- Doroudian B, Bagherimiyab F & Lemmin U. 2010. Improving the accuracy of four-receiver acoustic Doppler velocimeter (ADV) measurements in turbulent boundary layer flows. Limnology and Oceanography: Methods 8(11):575–591. https://dx.doi.org/10.4319/lom.2010.8.0575
- Garbini JL, Forster FK & Jorgensen JE. 1982. Measurement of Fluid Turbulence Based on Pulsed Ultrasound Techniques. Part 1. Analysis. Journal of Fluid Mechanics 118:445–470. https://dx.doi.org/10.1017/S0022112082001153
- García CM, Cantero MI, Niño Y & García MH. 2005. Turbulence Measurements with Acoustic Doppler Velocimeters. Journal of Hydraulic Engineering 131(12):1062-1073.https://dx.doi.org/10.1061/(ASCE)0733-9429(2005)131:12(1062)
- Goring DG & Nikora VI. 2002. Despiking acoustic Doppler velocimeter data. Journal of Hydraulic Engineering 128(1):117–126. https://dx.doi.org/10.1061/(ASCE)0733-9429(2002)128:1(117)
- Hurther D & Lemmin U. 2001. A Correction Method for Turbulence Measurements with a 3D Acoustic Doppler Velocity Profiler. Journal of Atmospheric and Oceanic Technology 18(3):446–458. https://dx.doi.org/10.1175/1520-426(2001)018<0446:ACMFTM>2.0.CO;2
- Khorsandi B, Mydlarski L & Gaskin S. 2012. Noise in Turbulence Measurements Using Acoustic Doppler Velocimetry. Journal of Hydraulic Engineering 138(10):829–838. https://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000589
- Kraus NC, Lohrmann A & Cabrera R. 1994. New Acoustic Meter for Measuring 3D Laboratory Flows. Journal of Hydraulic Engineering 120(3):406–412. https://dx.doi.org/10.1061/(ASCE)0733-9429(1994)120:3(406)
- Lemmin U & Rolland T. 1997. Acoustic Velocity Profiler for Laboratory and Field Studies. Journal of Hydraulic Engineering 123(12):1089–1098. https://dx.doi.org/10.1061/(ASCE)0733-9429(1997)123:12(1089)
- Liu M, Rajaratnam N & Zhu DZ. 2006. Mean flow and turbulence structure in vertical slot fishways. Journal of Hydraulic Engineering 132(8):765–777. https://dx.doi.org/10.1061/(ASCE)0733-9429(2006)132:8(765)
- Lohrmann A, Cabrera R, Gelfenbaum G & Haines J. 1995. Direct Measurements of Reynolds Stress with an Acoustic Doppler Velocimeter. Proceedings of the IEEE Fifth Working Conference on Current Measurement, IEEE Catalog Number 95CH35724, 205-210. https://dx.doi.org/10.1109/CCM.1995.516175
- MacVicar B, Dilling S, Lacey J. 2014. Multi-instrument turbulence toolbox (MITT): Open-source MATLAB algorithms for the analysis of high-frequency flow velocity time series datasets. Computers & Geosciences 73:88-98.
- Marriner BA, Baki ABM, Zhu DZ, Thiem JD, Cooke SJ & Katopodis C. 2014. Field and numerical assessment of turning pool hydraulics in a vertical slot fishway. Ecological Engineering 63:88-101. https://dx.doi.org/10.1016/j.ecoleng.2013.12.010
- McLelland SJ & Nicholas AP. 2000. A new method for evaluating errors in high-frequency ADV measurements. Hydrological Processes 14(2):351-366. https://dx.doi.org/10.1002/(SICI)1099-1085(20000215)14:2<351::AID-HYP963>3.0.CO;2-K
- Montero VGG, Romagnoli M, García CM, Cantero MI, Scacchi G. 2014. Optimization of ADV sampling strategies using DNS of turbulent flow. Journal of Hydraulic Research. 52(6), 862–869.
- Nortek. 2004. Nortek Vectrino Velocimeter. User Guide. Rev. C. Nortek AS, Norway.
- Odeh M, Noreika JF, Haro A, Maynard A & Castro-Santos T. 2002. Evaluation of the Effects of Turbulence on the Behavior of Migratory Fish. Final Report to the Bonneville Power Administration, Portland, Oregon. Contract 00000022, Project 200005700.
- Parsheh M, Sotiropoulos F &Porté-Agel, F. 2010. Estimation of power spectra of acoustic-Doppler velocimetry data contaminated with intermittent spikes. Journal of Hydraulic Engineering 136(6):368–378. https://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000202
- Puertas J, Pena L & Teijeiro T. 2004. Experimental approach to the hydraulics of vertical slot fishways. Journal of Hydraulic Engineering 130(1):10–23. https://dx.doi.org/10.1061/(ASCE)0733-9429(2004)130:1(10)
- Quaresma AL, Ferreira RML & Pinheiro AN. 2017. Comparative analysis of particle image velocimetry and acoustic Doppler velocimetry in relation to a pool-type fishway flow. Journal of Hydraulic Research. 55(4):582-591. https://dx.doi.org/10.1080/00221686.2016.1275051
- Quaresma AL, Romão F, Branco P, Ferreira MT, Pinheiro AN. 2018. Multi slot versus single slot pool-type fishways: a modelling approach to compare hydrodynamics. Ecological Engineering 122:197-206. https://doi.org/10.1016/j.ecoleng.2018.08.006
- Romão F, Quaresma AL, Branco P, Santos JM, Amaral S, Ferreira MT, Katopodis C & Pinheiro AN. 2017. Passage performance of two Cyprinids with Different Ecological Traits in a Fishway with Distinct Vertical Slot Configurations. Ecological Engineering. 105:180-188. https://dx.doi.org/10.1016/j.ecoleng.2017.04.031
- Santos JM, Branco PJ, Silva AT, Katopodis C, Pinheiro AN, Viseu T & Ferreira MT. 2012. Effect of two flow regimes on the upstream movements of the Iberian barbel (Luciobarbus bocagei) in an experimental pool-type fishway. Journal of Applied Ichthyology 29(2):425-430. https://dx.doi.org/10.1111/jai.12043
- Silva AT, Santos JM, Ferreira MT, Pinheiro AN & Katopodis C. 2011. Effects of water velocity and turbulence on the behaviour of Iberian barbel (Luciobarbus bocagei, Steindachner, 1864) in an experimental pool-type fishway. River Research and Applications 27(3):360–373. https://dx.doi.org/10.1002/rra.1363
- Voulgaris G & Trowbridge JH. 1998. Evaluation of the acoustic Doppler velocimeter (ADV) for turbulence measurements. Journal of Atmospheric and Oceanic Technology 15(1):272–289. http://dx.doi.org/10.1175/1520-0426(1998)015<0272:EOTADV>2.0.CO;2
- Wahl T. 2000. Analyzing ADV Data Using WinADV. Joint Conference on Water Resource Engineering and Water Resources Planning and Management. ASCE, Minneapolis, pp.1–10. https://doi.org/10.1061/40517(2000)300
Contact information
Nortek
e-mail: inquiry@nortekgroup.com
SonteK
e-mail: inquiry@sontek.com